For å forstå store tallmengder fra naturen må vi ofte bruke statistikk. I denne oppgaven skal vi bruke temperaturmålinger fra Gabriel til å regne på Grupperte data.

Oppgave

a) Last inn målinger av vanntemperatur i overflaten fra Gabriel for hvert dykk i en hel uke HER

Valg 1: "Vanntemperatur"
Valg 2: "Alle data i perioden"
Valg 3:  "06.20.07.2016-06.27.07.2016" (TT.DD.MM.ÅÅÅÅ)
Valg 4: "-0.5m"

Du vil nå få opp en .txt-fil med flere kolonner nedover (kolonner går nedover og rader går bortover). Kopier alle kolonner og rader i et nytt Excel ark.  Er målingene diskrete eller kontinuerlige variabler?

Dersom du har problemer kan du se DENNE videoen om hvordan man laster inn og plotter data fra Gabriel i Geogebra.

b) For å oppnå en mer oversiktlig og informativ fremstilling av innhentet datasett, er det vanlig å gruppere tallmaterialet. Følg steg for steg følgende fremgangsmåte for gruppering av oseanografiske data:

• Bestem maksimum og minimum.
  Finn minste og største observasjons verdi
• Del inn i k-klasser.
  Vi deler temperaturområdet inn i k-klasser med like brede klasseintervaller. La klasseintervallene ha en bredde som tilsvarer 2 grader celsius. Klassene må ikke overlappe hverandre, og til sammen må klassene dekke alle verdiene fra maksimum til minimum.
• Lag en frekvens - tabell
  Tabellen skal inneholde følgende kolonner:
  • Klasseintervall
  • Klassemidtpunkt
  • Frekvens
  • Relativ frekvens
  • Kumalativ frekvens
  • Relativ kumulativ frekvens
  • [latex]{m_i * f_i} [/latex]
  • [latex]{m_i^2 * f_i}[/latex]

c) Bruk følgende formler til å finne gruppert middelverdi og gruppert standardavvik:

Gruppert middelverdi: [latex] {\bar{x}_g=\frac{1}{n}\displaystyle\sum_{i=1}^{k}m_i*f_i }[/latex]

Gruppert standardavvik: [latex]{ s_g= \sqrt{\frac{1}{n}\displaystyle\sum_{i=1}^{k}(m_i-\bar{x}_g)^2f_i}} [/latex]

d) Lag et relativ frekvens-histogram for dataene du grupperte i forrige oppgave.

e) Last inn nye målinger av vanntemperatur og saltholdighet fra et bestemte dykk (vertikale profil).

Fil 1:
Valg 1: "Vanntemperatur"
Valg 2: "Alle data i perioden"
Valg 3:  "06.20.07.2016-09.20.07.2016" (TT.DD.MM.ÅÅÅÅ)
Valg 4: "Alle dyp"

Fil 2:
Valg 1: "Saltholdighet"
Valg 2: "Alle data i perioden"
Valg 3:  "06.20.07.2016-09.20.07.2016" (TT.DD.MM.ÅÅÅÅ)
Valg 4: "Alle dyp"

Kopier begge radene av salt og temperatur inn i et Excel ark. For hvert av de to dykkene se på temperatur og saltholdighet som hører sammen og plot disse i ett punktdiagram der temperaturen tilsvarer x-aksen og saltholdigheten tilsvarer y-aksen. Vi kaller et slikt diagram for et T-S plot og det blir mye brukt av havforskere for å studere vannmasser.

f) Gjenta oppgave e) men isteden for å bare laste inn en profil last inn gjennomsnittlige døgnprofiler for 7 dager. Plot alle temperatur og saltholdighet målinger i samme T-S plot der temperaturen tilsvarer x-aksen og saltholdigheten tilsvarer y-aksen.

Fil 1:
Valg 1: "Vanntemperatur"
Valg 2: "Døgnmiddel" (Gjennomsnitt av alle profiler i løpet av et døgn)
Valg 3:  "06.20.07.2016-06.27.07.2016" (TT.DD.MM.ÅÅÅÅ)
Valg 4: "Alle dyp"

Fil 2:
Valg 1: "Saltholdighet"
Valg 2: "Døgnmiddel" (Gjennomsnitt av alle profiler i løpet av et døgn)
Valg 3:  "06.20.07.2016-06.27.07.2016" (TT.DD.MM.ÅÅÅÅ)
Valg 4: "Alle dyp"

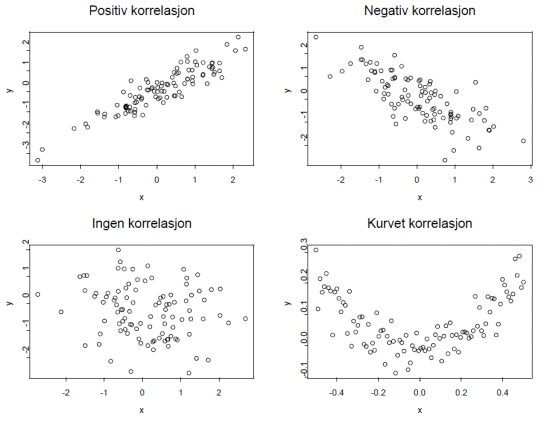
g) Kan du se et mønster i punktdiagrammet du laget i oppgave f) ? Kan du se noe korrelasjon eller gjette en r-verdi?